Abnormitäten

Übersicht Merkmale

Abnormitäten

Gelegentlich weist das Flügelgeäder Fehler oder Unregelmäßigkeiten auf (Abb.34). Für die Beurteilung fallen solche abnormen Flügel natürlich aus. Es ist daher ratsam, zusätzlich einige Flügel je Probe zu präparieren, um auf diese zur Bewertung ausweichen zu können. Abnormitäten treten bei einigen Zuchtlinien relativ häufig auf. Eine solche Beobachtung sollte man auf dem Auszählbogen vermerken.

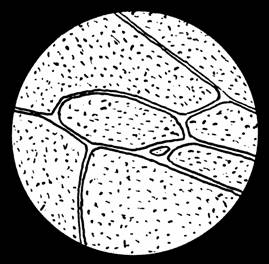
Abbildung 34
Abnormität des Flügelgeäders

Temperatureinflüsse

Die Ausgestaltung des Flügelgeäders wird nach SOOSE in hohem Maße durch die Temperatur beeinflußt. Unterkühlung der Bienenbrut während ihrer Entwicklungszeit bedingt eine Verkleinerung, Temperaturerhöhung dagegen eine Vergrößerung des Indexwertes. Es ist bekannt, daß sich in einem Volk der Bienenschlupf häufig verzögert, weil die Brut in der Entwicklungszeit abweichenden Temperaturen, meist einer Abkühlung, ausgesetzt war. Das ist besonders bei Witterungsrückschlägen und nach dem Umhängen von Brut der Fall. Nach Eingriffen ins Brutnest im zeitigen Frühjahr gezogene Proben müssen sehr kritisch beurteilt werden. Das gleiche gilt für Proben aus schlecht isolierten Begattungskästchen (EWK) für die Vorkörung.

Variationskurve und Berechnung des Mittelwertes

Das Verhältnis der beiden Teilstrecken a zu b (Cubitalindex) erhält man durch Division a/b (a:b).

Die Berechnung erfolgt auf zwei Stellen hinter dem Komma. Beim Projektionsverfahren und dem Indexfächer nach HEROLD liest man die Verhältniszahl als Indexwert direkt ab, damit erspart man sich das Ausrechnen. Mit Hilfe der Indexwerte kann man Variationskurven erstellen, die wertvolle Aufschlüsse über Reinpaarung und Vererbungstreue ergeben.

Zu diesem Zweck werden die ermittelten Indexwerte in Klassen eingeteilt (nach RUTTNER):

Indexwert Klasse Indexwert Klasse

Von – bis von - bis

0,70 - 0,75 1 2,00 - 2,15 16

0,76 - 0,80 2 2,16 - 2,32 17

0,81 - 0,86 3 2,33 - 2,52 18

0,87 - 0,92 4 2,53 - 2,74 19

0,93 - 0,99 5 2,75 - 2,99 20

1,00 - 1,06 6 3,00 - 3,28 21

1,07 - 1,13 7 3,29 - 3,61 22

1,14 - 1,21 8 3,62 - 3,99 23

1,22 - 1,30 9 4,00 - 4,44 24

1.31 - 1,39 10 4,45 - 4,99 25

1,40 - 1,49 11 5,00 - 5,66 26

1,50 - 1,60 12 5,67 - 6,49 27

1,61 - 1,72 13 5,50 - 7,56 28

1,73 - 1,85 14 7,57 - 8,99 29

1,86 - 1,99 15 9,00 - 30

Indexwerte nach Klassen

Für das Projektionsverfahren wurde ein Indexfächer entwickelt, auf dem die Indexklasse statt des Indexwertes abgelesen werden kann. Dieser Indexfächer befindet sich im Anhang dieses Buches bei den Formularen. Für den Gebrauch kopiert man sich den Fächer zweckmäßiger Weise auf ein stärkeres Papier oder einen Karton. Weitere Exemplare können vom DIB bezogen werden.

Wenn man mit einem Mikrofilm-Lesegerät arbeitet, kopiert man den Indexfächer auf eine durchsichtige Folie (verkleinert), die man direkt auf den Bildschirm legt. Mit dem Indexfächer kann man sich die Ausrechnung sparen, dadurch sehr rasch arbeiten, und die Indexklassen direkt auf dem Auszählbogen eintragen. In Form einer Variationsreihe gibt man dabei die jeder Klasse zugeordnete Zahl der Bienen bzw. der Flügel an,

Beispiel:

Klasse: 15 16 17 18 19 20 21 22

Zahl der Bienen -- -- 2 6 15 16 9 2

Es ist jedoch übersichtlicher, die Werte in Form einer Variationskurve aufzutragen. Man trägt auf der waagerechten Koordinate die Klasse und auf der senkrechten die Bienenzahl ein. Die Verbindung der Einzelwerte durch Linien ergibt eine Kurve, die Variationskurve (Abb.35)

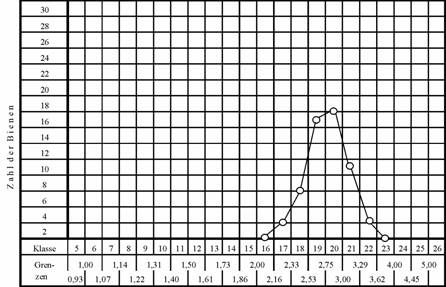
Abbildung 35
Variationskurve des Cubitalindex

Wenn man mit kariertem Papier arbeitet und für jede Biene in einer Klasse ein Karo ankreuzt, kommt man schneller zur gleichen Kurve. Auf den Merkmalsuntersuchungsbögen des DIB sind solche Felder bereits vorgedruckt. Das Zuordnen der Indexwerte zu den Klassen und das Ankreuzen kann gleichzeitig erfolgen, wodurch man die gewünschte Kurve rasch in Form eines Stufendiagramms erhält (Abb. 36). In der Variationsstatistik nennt man eine solche Darstellung „Treppenpolygon“.

Zur Beurteilung eines Volkes ist neben der Indexkurve auch der Mittelwert aller gemessenen Indexwerte erforderlich. Er ergibt sich aus der Summe aller Mittelwerte, dividiert durch die Anzahl der untersuchten Bienen.

Gren-

0,87

1,00

1,14

1,31

1,50

1,73

2,00

2,33

2,75

3,29

4,00

5,00

6,50

zen

0,93

1,07

1,22

1,40

1,61

1,86

2,16

2,53

3,00

3,62

4,45

5,67

Klasse

Cubitalindex nach Klassen (bezogen auf 1/60 Teilstrecke)

Abbildung 36
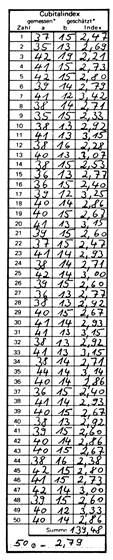
Spalte mit Ablesewerten, errechneten Indexwerten sowie Stufendiagramm.
(Auszug aus Auszählbogen des DIB)

Da in der Regel 50 Flügel für eine Probe untersucht werden, ergibt sich folgende Formel für den Mittelwert:

M =	Summe aller Indexwerte
	50

Mit dem korrigierten Indexfächer nach HEROLD liest man nicht die Indexwerte, sondern die Indexklassen ab. Hier muß der Wert über den Klassenmittelwert errechnet werden. Da der Durchschnitt der Proben nicht am Anfang sondern im Mittel einer Klasse liegt, zählt man zum Klassenmittel noch eine halbe Klasse, also den Wert 0,5 hinzu, das ergibt für den Klassenmittelwert die Formel:

M =	Summe aller Indexwerte	+ 0,5
	50

Beispiel:	Anzahl der Bienen	Klasse
	2	17	=	34
	6	18	=	108
	15	19	=	285
	16	20	=	320
	9	21	=	189
	2	22	=	44
Gesamtsumme				980

Klassen-Mittelwert M = 980 : 50 = 19,6 + 0,5 = 20,10

Dieser Wert wird im Diagramm direkt als senkrechte Linie eingetragen.

Unter Mittelwert als Klasse kann man sich nicht allzu viel vorstellen. Man muß ihn daher in einen realen Wert umrechnen. Für den Klassenwert setzt man den unteren Grenzwert ein und gewinnt durch Interpolation den weiteren zu addierenden Wert. Man multipliziert die Differenz zur nächsten Klasse mit dem Klassenmittel hinter dem Komma, das ergibt den realen Mittelwert.

Beispiel: Klassen-Mittelwert (s.o.) 20,10. Die Klasse 20 beginnt mit 2,75 und reicht bis 2,99, die Differenz beträgt also 0,24. Durch Interpolation erhält man nun den realen Mittelwert: M = 2,75 +(0,10x0,24) = 2,75+0,02 = 2,77

Seite zurück